一般来说,我们希望我们通过训练得到的模型更多地是学习到了一种模式,而不是只是单纯地对历史数据的存粹记忆。
从直觉上来说,如果一个模型能够完美复刻所有的历史数据(也就是说训练误差很小),那么它的泛化能力一定不会很优秀(其实这只是直觉上的,并不一定是对的)
一般来说,数据量越大,模型的复杂度越高(参数量和参数的取值范围越大),那么模型的泛化能力就会越好
训练误差和泛化误差
整体前提:训练数据和测试数据是独立同分布的,因为如果不这样做的话,那么我们根本无法从测试误差中得到任何有效的、可以反映训练误差的内容。
训练误差
简单来说,训练误差指的就是根据损失函数计算出来的样本总体损失的平均值
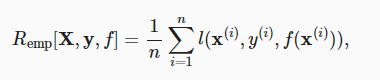
其中X表示样本特征,y表示样本标签,f表示损失函数
泛化误差
对于泛化误差,首先要明确一个前提,即我们认为面对一个具体的任务,模型需要学习的数据本身是存在一个特定分布的,这个分布有可能非常非常难以理解和表示,但是整体上数据符合这个分布。
从上述观点出发,泛化误差可以表示为:
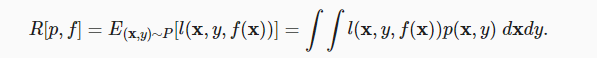
其中p(x,y)表示前文中提到的数据符合的分布的概率密度函数
由于我们无法得知这个概率分布究竟是什么,所以我们一般使用测试误差代替泛化误差
由于模型的选择不同,训练误差会据此在泛化误差附近波动,泛化问题的关键就是到底怎么样才能说我们的训练误差和泛化误差接近
The central question of generalization is then when should we expect our training error to be close to the population error (and thus the generalization error)
模型复杂度
模型复杂度的决定因素有很多,也很复杂。
某种程度上来说是由模型的参数数量来决定的,而大部分情况下,模型复杂度是由参数的取值范围决定的
欠拟合和过拟合
欠拟合
训练误差很大
过拟合
训练误差很小,测试误差很大
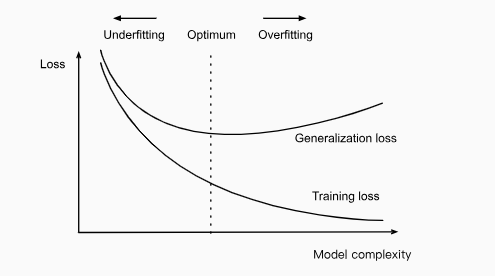
上图很好的解释了模型复杂度和误差之间的关系,注意这里有一个前提,那就是喂给模型的数据量保持不变。
如果模型能够得到的数据很少,那么深度神经网络解决问题的能力(泛化能力)甚至不如简单的线性模型!
训练集,验证集,测试集
在理想的条件下,测试集应该只被使用一次,用于测试完成训练后的模型的泛化能力
一定要注意的是,我们不能通过测试数据来训练模型!!!其原因是显而易见的,如果说我们都同意使用测试误差来代替泛化误差,那么我们一旦使用测试集训练神经网络,我们又如何能够得知真正的泛化误差呢?
在训练过程中需要对超参数进行调优,一般使用验证集完成这个需求
回到测试集的问题上,现实训练中可能根本没有充分的数据,所以只使用一次的测试集只存在于理论中,一种解决方式是使用K层交叉验证
K层交叉验证
将预处理后的数据分为不重叠的k组,每次挑选一组作为验证集,其余分组用于训练,重复直到每个分组都被作为过验证集。最后计算总训练和测试误差的平均值。
在了解了基本的泛化问题后,进一步地,我们考虑如下问题:
- 测试集中的样本数需要达到多少,我们才可以自信地说,模型在测试集中得到的误差可以代表泛化误差?
- 如果我们在一个测试集上连续测试多个分类器的性能会发生什么?
- 我们为什么有把握认为通过训练得到的,拟合后的分类器比起最原始的乱猜分类的泛化能力要更强呢?
重新审视测试集
我们做出如下假设,假设测试集中的样本数据与模型需要解决的问题的整体数据的概率分布独立同分布(有点像测试集中的数据是从整体中抽样出来的),那么根据概率论给我们的知识
如果测试集中的数据满足均值为u,方差为 kesi 的概率分布,那么随着样本数n的不断提升,根据中心极限定理,这个n个样本的和应该符合均值为nu, nkesi的正态分布,慢着,当n接近无穷大时,我们不就可以近似地把测试集看作整体数据了吗
也就是说,从统计量可以反映总体的均值和方差角度出来,测试集(样本)的平均值,符合均值u, 方差kesi / √n 的正态分布。 其中u和kesi与总体的u和kesi相同!!!
也就是说,为了保持测试集数据与总体样本数据的变化范围(我们 知道这个值由方差描绘)保持小范围的浮动,举例来说,保持正负0.01的浮动,我们需要n提升10000倍,也就是样本数据需要达到10000!
多重假设检验
具体来说,如果我们首先设计一个模型f, 它在测试集上表现出了不错的性能,但是我们并不满足它的表现,因此我们根据验证集所体现出来的误差对模型f进行超参数调优,设计出了一个新的模型f2, 并在同一个测试集上对它进行性能测试,得出了更好的结果,可是,这个结果我们真的能相信吗?
事实上,当你根据在一个测试集上测试得出的结果进行参数调优时,这个测试集中的隐含信息就已经被泄露给你了,换句话说,现在知道这些信息不再是模型本身,而是你自己,你又根据这些信息优化了模型,等同于模型知道了测试集中数据。因此这个模型存在过拟合风险。
如果你因为读到这而感到灰心,或者说更加执着于设计一个更加完美的测试集,那倒也并无必要,想象一下,在现实情况下,我们可能根本没有如此巨量的数据可以让我们分出很多模型永远没有遇见过的测试集数据,或者说换个思路,除非你从头开始收集数据集,那么你从已有数据集中分离出来的测试集,早就可能被别人测试过了,你在前人提出模型的基础上改进得来的模型可能早就已经得到了一些测试集中的信息。
我们一般只需要在数据量比较小,风险较高的情况下注意这个问题即可。
目前比较可行的解决方法是,当迭代一定轮次后,将老久的测试集中当作直接作为新的验证集,另选择一个提前准备好的备用测试集作为新的测试集。
