极大似然估计
我们首先来了解两个概念:预测和估计
预测是指根据参数(可以理解为模型中的每个参数都已知),去推断未来发生的事件
预测是由因到果,预测发生的可能性称之为概率
例子:已知一枚硬币是均匀分布的,推测抛100次硬币后,正面和反面各出现的次数
估计是指根据观测到的样本结果,去反推模型中的参数p
估计是预测的逆过程,是执果索因,估计参数p正确的可能性称之为似然性
似然性的计算几乎和概率的计算一致,只不过由于p现在是未知的,样本结果的取值现在已知
例子:已知抛一百次硬币的结果为正面70次,反面30次,推断抛硬币模型中对应的概率分布中的p值
现在规定似然函数:
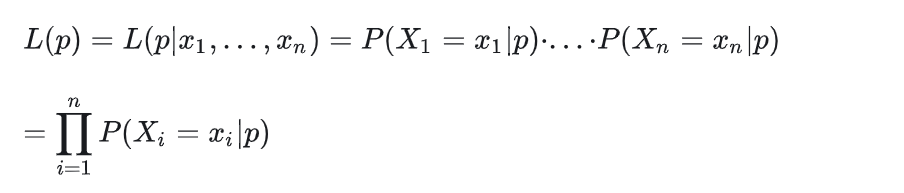
所谓极大似然,就是求一个p, 使似然函数最大,也就是说,从已经发生的结果出发,取这个p值,符合原分布的p值的可能性是最大的!
softmax回归
和线性回归模型一样,还是使用全连接层,只不过当我们需要输出q个类别的预测值时,权重矩阵需要做出改变:
考虑一个样本有m个特征,那么输出一个类别的预测就需要m个权重参数,累乘后再加上一个偏置b, 如果类别数拓展到q个,那么权重矩阵就需要 m * q 个参数
模型的神经网络结构如下:
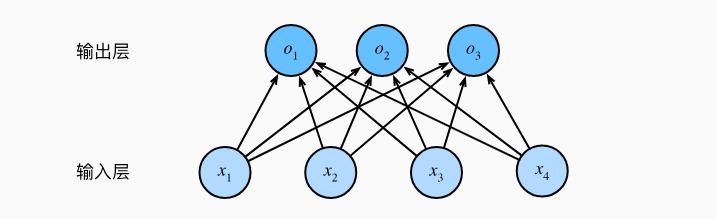
此时神经网络输出的预测值并不规范(不能代表概率),具体体现在:
- 预测的值不一定满足大于0小于1
- 预测值总和不一定为1
使用softmax函数对预测值进行规范化:

Y_hat是预测的整个向量,Yj_hat是向量中的分量
矢量化操作
采用矢量化操作,特征矩阵X的形状拓展到 n *m (其中n表示样本个数,m表示单个样本的特征数)
权重矩阵W对应为 m * q (q表示分类器的类别数)
注意这里的权重矩阵W中的每个列向量对应的才是单个类别的权重参数!!!
偏置矩阵B拓展到 1*q
注意这里是一个行向量!!!可以这样理解,每行代表一个样本,每行中的每列代表每个类别的预测概率)
整个softmax回归的矢量表达式变为:
O = XW + B
Y_hat = softmax(O)
交叉熵损失
如果我们在分类问题中仍然使用平方差损失函数(BSELoss),能不能使模型拟合?答案是可以,但是没必要,平方差损失对于数值要求实在是太高了,例如预测输出如果是(0.1,0.2,0.7),那么它和预测输出(0.2,0.2,0.6)输出的类别是一致的,但是显然为了达到后者的精度,拟合的代价是过高的。
在这里引入交叉熵损失
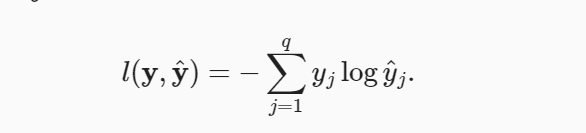
由于规定标签y是一个独热向量(即向量中只有一个1,其余全为0),所以分类问题中的交叉熵函数其实就是为了降低不正确分类的值,提升正确分类的值
交叉熵只关心对图像中出现的物体类别的预测概率。最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率
训练过程
在这里,正式给出神经网络的训练过程模板:
针对每一个迭代周期:
- 首先从训练集中取出一个小批次的样本
- 将样本特征放入已经初始化参数的模型中,得到预测结果
- 根据损失函数计算损失,反向传播计算梯度,使用梯度下降优化算法更新模型的权重
- 重新从训练集中取出一个批次的样本,重复上述过程,直到整个训练集中的样本都被遍历
- 结束本次迭代,开始下一次迭代
当遇到最后一个批次的样本值达不到指定的批量大小时,舍弃这个批次即可
