自动微分

粗略的理解：深度学习框架会根据设计好的模型，得到一张计算图，计算图中描绘了哪些数据通过哪些组合产生了输出，通过计算图，框架可以进行反向梯度传播，计算每个参数的偏导数

x = torch.arange(4.0, requires_grad = True)
y = 2 * torch.dot(x,x)
y.backward()
x.grad

非标量函数的反向传播

注意到，上述函数的结果是一个标量

但是当结果是一个非标量时我们该怎么做？

例如：如果输出的是一个向量，矩阵，张量？

x.grad.zero_()#首先清除存储的梯度
y = x * x 
y.sum().backward()
#这里实际上是提供了一个形状为（Xn, 1）的全1张量作为梯度参数（grad_tensors）
x.grad

有关于grad_tensors参数的解释详见：

https://zhuanlan.zhihu.com/p/83172023

自动微分机制详解（大概）

引用自：https://zhuanlan.zhihu.com/p/69294347

首先来了解一下pytorch中的计算图机制，若有以下定义：

input = torch.ones([2, 2], requires_grad=False)
w1 = torch.tensor(2.0, requires_grad=True)
w2 = torch.tensor(3.0, requires_grad=True)
w3 = torch.tensor(4.0, requires_grad=True)

l1 = input * w1
l2 = l1 + w2
l3 = l1 * w3
l4 = l2 * l3
loss = l4.mean()

loss.backward()
#或者 torch.autogard.backward(loss)

pytorch内部会自动生成一张正向传播的计算图：

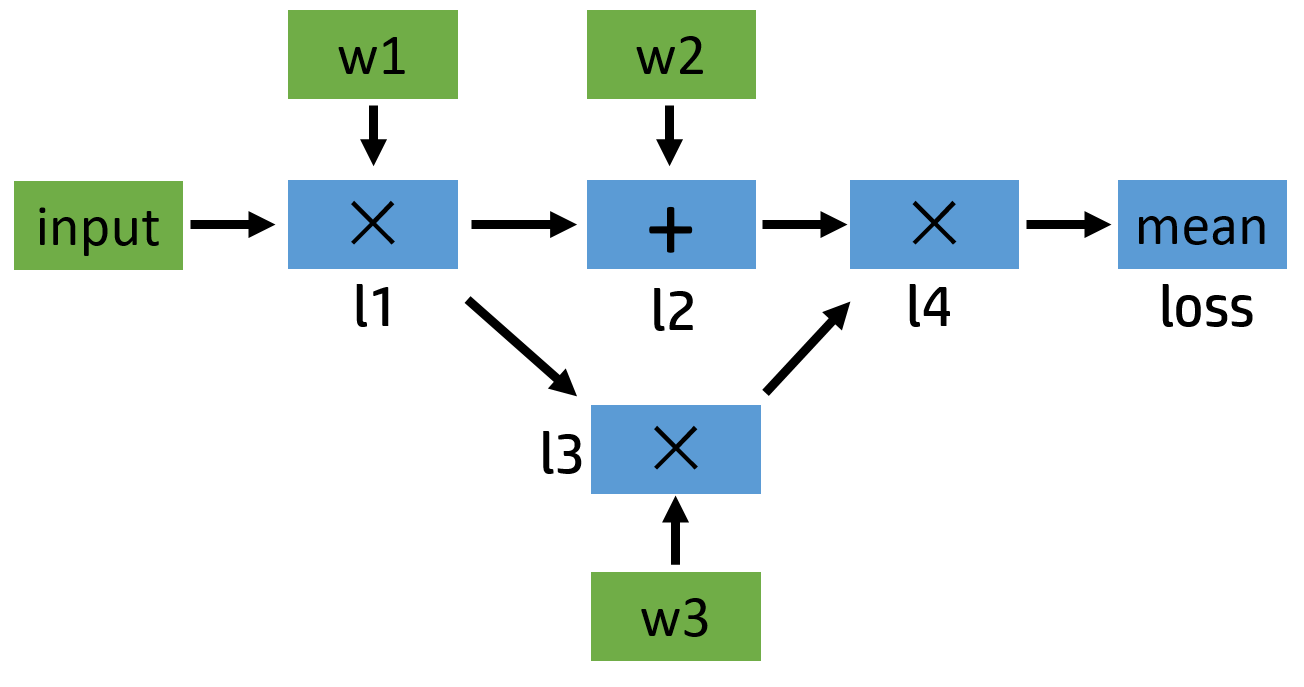
接下来是反向传播的计算图：

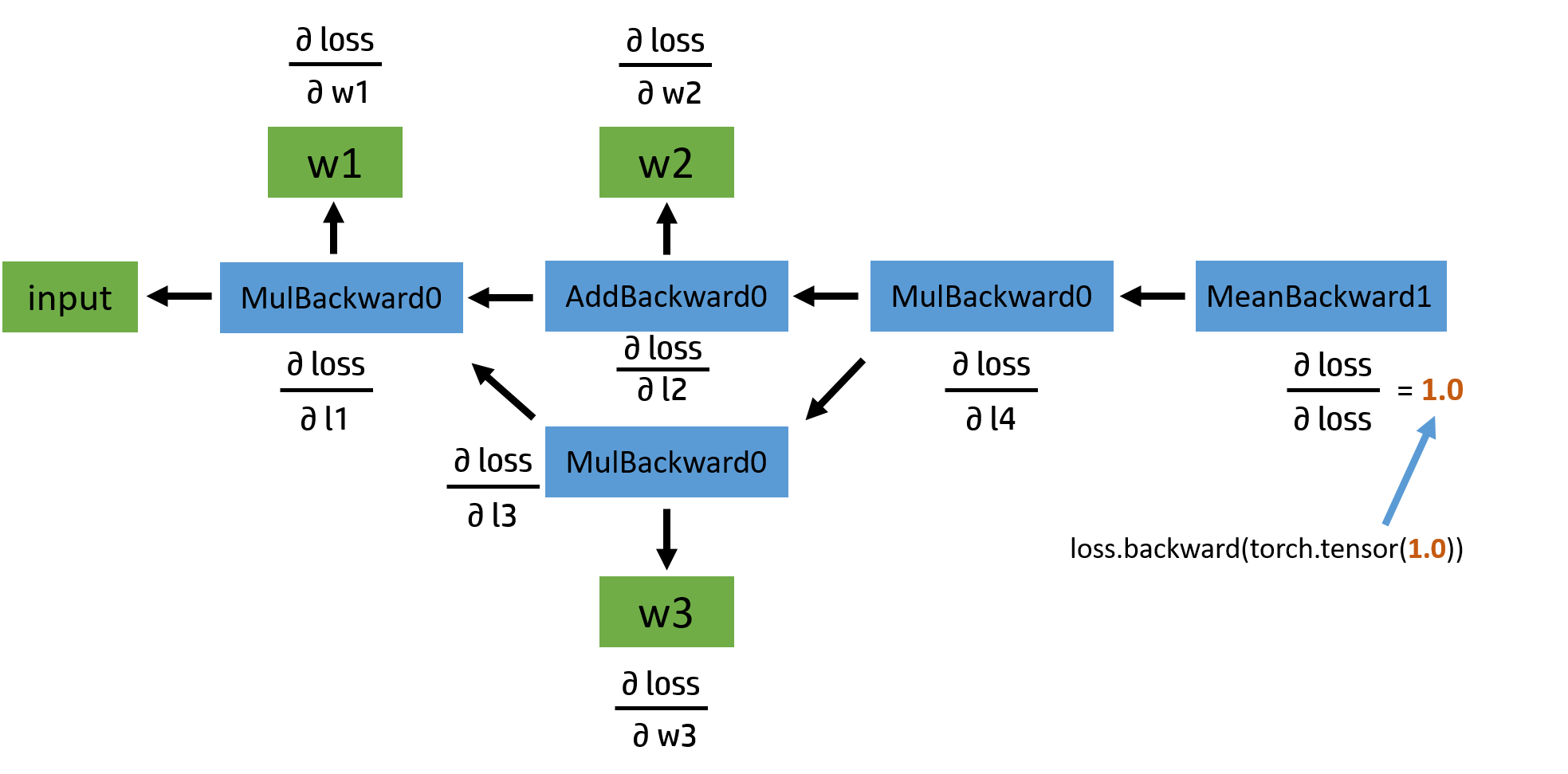
其实所谓的反向传播就是根据链式求导法则，从输出节点开始，一步一步的反向求导（偏导），直到获取到输入节点的梯度值。

一般来说，自动微分机制与梯度下降优化算法相关联，当我们获取到权重w的梯度向量后，可以沿梯度方向下降以最快寻找到整个损失函数的局部最小点，从而达拟合模型。

理解了什么是计算图后，再来了解一下计算图中的各个节点

叶子节点与非叶子节点

首先列举一下tensor中记录的各项属性：

• data: 即存储的数据信息
• requires_grad: 设置为True则表示该Tensor需要求导
• grad: 该Tensor的梯度值，每次在计算backward时都需要将前一时刻的梯度归零，否则梯度值会一直累加，这个会在后面讲到
• grad_fn: 叶子节点通常为None，只有结果节点的grad_fn才有效，用于指示梯度函数是哪种类型。例如在反向传播图中的MulBackward()等
• is_leaf: 用来指示该Tensor是否是叶子节点

引用自：https://zhuanlan.zhihu.com/p/83172023

判断一个tensor是否是叶子节点，本质是看is_leaf的值

但是，在日常使用中，如何快速判断一个tensor节点是否是叶子节点呢？

一般来说，作为我们自己创建的tensor, 并且指定了requires_grad = True,这类节点都是叶子节点

由上述自己创建的tensor通过各类操作运算得到的节点，一般被称为中间节点，这类节点都是非叶子节点

需要注意的是，中间节点在反向传播过程中是不保存导数值的（梯度值），计算图反向传播后也会直接自动销毁

如果我们想要查看中间节点的导数值，可以使用如下方法：

#方法一： 在反向传播前，对中间节点使用retain_grad()方法
l1.retain_grad()
l4.retain_grad()
loss.retain_grad()

loss.backward()

#方法二： 使用pytorch的register_hook钩子函数，这种方法只是显示梯度值，并不进行存储
l1.register_hook(lambda grad: print('l1 grad: ', grad))
l4.register_hook(lambda grad: print('l4 grad: ', grad))
loss.register_hook(lambda grad: print('loss grad: ', grad))

loss.backward()
#注意！在这之后如果继续访问中间节点的梯度值，是会报错的！

叶子节点与就地操作

就地操作（inplace operation）:在前文中提到过，是指不开辟新的内存空间，直接修改引用指向的内存中的值

如果针对计算图中的节点进行就地操作，在pytorch中会带来两种问题：

1. 对于非叶子节点进行就地操作（这个非叶子节点参与了偏导数的计算），会报：

   RuntimeError: one of the variables needed for gradient computation has been modified by an inplace operation …

2. 对于叶子节点进行就地操作，会报：

   RuntimeError: a leaf Variable that requires grad has been used in an in-place operation.

   针对叶子节点的情况，在反向传播前，不允许任何对于叶子节点的直接就地操作！

想一想，为什么torch中对于计算图中节点，严格要求不允许就地操作呢？

仔细思考一下，如果有一个变量的值在参与正向传播后，值被修改了，当我们需要进行反向传播时，我们如何得知原来的值呢？

一旦计算图中的一个值是不确定的，其后果是灾难性的，其反向的所有节点的梯度值都将无法计算！

torch通过_version属性来判断tensor是否进行过就地操作：

a = torch.tensor([1.0, 3.0], requires_grad=True)
b = a + 2
print(b._version) # 0

loss = (b * b).mean()
b[0] = 1000.0
print(b._version) # 1

loss.backward()

那么如何绕过torch的检测机制，修改模型中的w权重呢？

# 方法一
a = torch.tensor([10., 5., 2., 3.], requires_grad=True)
print(a, a.is_leaf, id(a))
# tensor([10.,  5.,  2.,  3.], requires_grad=True) True 2501274822696

a.data.fill_(10.)
# 或者 a.detach().fill_(10.)
print(a, a.is_leaf, id(a))
# tensor([10., 10., 10., 10.], requires_grad=True) True 2501274822696

loss = (a*a).mean()
loss.backward()
print(a.grad)
# tensor([5., 5., 5., 5.])

# 方法二
a = torch.tensor([10., 5., 2., 3.], requires_grad=True)
print(a, a.is_leaf)
# tensor([10.,  5.,  2.,  3.], requires_grad=True) True

with torch.no_grad():
    a[:] = 10.
print(a, a.is_leaf)
# tensor([10., 10., 10., 10.], requires_grad=True) True

loss = (a*a).mean()
loss.backward()
print(a.grad)

如何求二阶导

如果我们想要求二阶导，则在使用backward方法时，把retain_graph设置为true, 这会导致计算图在完成反向传播计算后并不马上自动销毁，值得注意的是这会加剧对内存的消耗